Remember that time you tried to understand the intricacies of computer programming, only to get lost in a sea of 0s and 1s? Binary, the language of computers, seemed like a baffling code. But what if I told you there are other number systems that can simplify things, offering a more human-readable way to represent those digital values? Enter the fascinating world of hexadecimal and octal number systems, two close cousins of binary, often used in computer science and engineering.

Image: yodack.com
These systems are not just academic curiosities. They are vital tools for programmers, hardware engineers, and even everyday tech enthusiasts. Understanding their structure and applications can de-mystify the digital world, enhancing your understanding of how computers work and how they interact with us. So, let’s dive into the world of hexadecimal and octal, unravel their secrets, and see how they make our digital lives a little less binary.
Beyond Binary: Exploring the Hexadecimal and Octal Number Systems
In our daily lives, we’re accustomed to the decimal system, which uses ten digits (0-9) and place values based on powers of ten. However, computers rely on binary, a system that uses only two digits (0 and 1) and powers of two. While binary is fundamental to computers, it can be cumbersome for humans to handle, especially when dealing with large numbers. This is where hexadecimal and octal come into play.
Hexadecimal: Representing Binary with Efficiency
Hexadecimal (often shortened to “hex”) uses 16 unique symbols (0-9 and A-F) to represent numbers. Each digit in a hexadecimal number has a place value that is a power of 16. The key to understanding hexadecimal’s power lies in its relationship with binary: each hexadecimal digit conveniently represents four binary digits (a nibble). This efficiency makes hexadecimal a popular choice for representing memory addresses, color codes (in web design), and other binary values in a more compact and readable way.
Octal: A Simpler Approach to Binary
Octal, on the other hand, utilizes 8 unique symbols (0-7) and place values based on powers of eight. Each octal digit represents three binary digits. While octal’s representation of binary is less space-efficient compared to hexadecimal, it is considered more straightforward and easier to learn. Octal is commonly used for representing file permissions in Unix-based operating systems and in some older computer architectures.
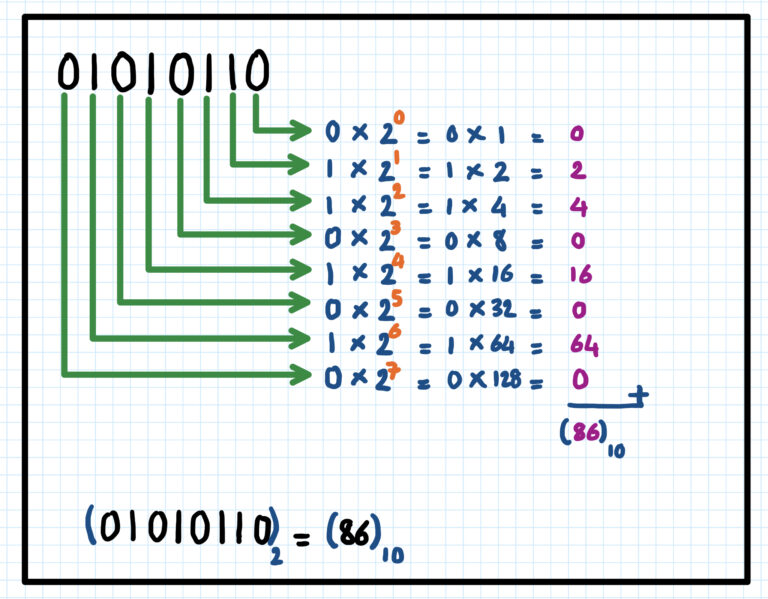
Image: kenanhancer.com
From Binary to Hexadecimal and Octal: A Step-By-Step Conversion
Converting between binary, hexadecimal, and octal is crucial for understanding how these systems interact and how they are used in various applications. Let’s take a closer look at the conversion process:
Binary to Hexadecimal:
- Group the binary digits into sets of 4 (from right to left), adding leading zeros if necessary.
- Convert each group of 4 binary digits into its equivalent hexadecimal digit.
- Combine the hexadecimal digits in the same order as the binary groups.
Binary to Octal:
- Group the binary digits into sets of 3 (from right to left), adding leading zeros if necessary.
- Convert each group of 3 binary digits into its equivalent octal digit.
- Combine the octal digits in the same order as the binary groups.
Hexadecimal and Octal to Binary:
- Convert each hexadecimal or octal digit into its equivalent binary representation (4 bits for hexadecimal, 3 bits for octal).
- Combine the binary representations in the same order as the original hexadecimal or octal digits.
The Modern Relevance of Hexadecimal and Octal
Despite the rise of higher-level programming languages, hexadecimal and octal remain relevant in various modern applications. Programmers and engineers still use them for tasks such as:
- Memory Management: Hexadecimal is particularly useful for representing memory addresses, which can be quite lengthy in binary.
- Low-Level Programming: These systems find application in languages like assembly language that involve direct interaction with hardware.
- Hardware Engineering: Hexadecimal is often employed for describing hardware registers, color codes, and other device configurations.
- Networking: IP addresses are sometimes displayed in hexadecimal format, particularly when working with network protocols.
- Data Representation: Hexadecimal format is frequently used in representing data formats, like color codes in web design or data encryption.
Expert Tips for Mastering Hexadecimal and Octal
Learning hexadecimal and octal can unlock a new level of understanding about how computers work, opening up exciting possibilities in programming and hardware engineering. Here are a few tips to accelerate your learning curve:
Practice Conversion: Frequent conversion exercises between binary, hexadecimal, and octal will solidify your understanding. You can find online tools or create your own worksheets for this purpose.
Explore Real-World Applications: Seek out examples of hexadecimal and octal usage in real-world situations. This will reinforce their relevance and practical value. Browse through assembly language code snippets, explore web design tutorials that use hexadecimal color codes, or investigate the inner workings of networking protocols.
FAQs about Hexadecimal and Octal Number Systems
Q: Why do we need different number systems?
Different number systems have different advantages and disadvantages. While binary is the native language of computers, it’s not always the most efficient or human-friendly system to work with. Hexadecimal and octal provide a more compact and readable representation of binary, making it easier for programmers and engineers to work with large amounts of data.
Q: What is the biggest difference between hexadecimal and octal?
The main difference lies in their base: hexadecimal uses base 16, whereas octal uses base 8. As a result, each hexadecimal digit represents four binary digits, while each octal digit represents three.
Q: Are these systems only useful for programmers?
While these systems are widely used in computer programming, they can also be valuable for anyone interested in understanding the fundamentals of how computers work. Knowing about these systems can enhance your understanding of technology in general.
Q: Can I learn these systems without extensive programming experience?
Absolutely! Learning hexadecimal and octal is within reach even for beginners. You can start with basic conversion exercises and gradually explore their applications in various scenarios.
2.3.1 Hexadecimal And Octal Number Systems
Conclusion: The Journey Beyond Binary
Stepping beyond the realm of binary into the world of hexadecimal and octal opens new doors for understanding the inner workings of computers and technology. It is not simply a matter of memorizing digits. It is about developing a deeper grasp of how these systems interact, influencing how we work with computers and how technology shapes our lives.
Are you intrigued by the prospect of delving deeper into these fascinating number systems? What sparked your interest in understanding hexadecimal and octal? Let’s continue this exploration together and unlock the mysteries of binary’s cousins!






